
 Introduction to
Naval Weapons Engineering
Introduction to
Naval Weapons EngineeringInfrared Propagation and Detection
In this section, we take up the problem of detecting and locating
a target by the collection and processing of its thermal radiation.
This is considered a passive process because the source
of the radiation is the target itself. An active system,
on the other hand, uses a separate source and detects the energy
which is reflected off the target. For example, radar is an active
system. Passive systems cannot measure range directly, because
there is no means of determining the time delay between emission
and reception like in radar systems, for example. However, passive
systems do have the great advantage of being covert, meaning they
do not necessarily give away their location in the process of
detecting a target.
Electro-optical detecting systems involve the process
of collecting and measuring the radiation from the target. In
general, this process is called radiometry. Since we will
be using many of the same principles to study how weapons systems
employ electo-optics, we will adopt the standard terminology used.
The following common radiometric terms and symbols will prove
useful:
Flux, F. The rate of energy
flow per unit time, which, of course, is power. Therefore, flux
has the same units as power, namely Watts (W). The term flux
may be applied either to the power leaving the target or to the
power which is collected by the detector.
Exitance, M. The flux per unit area of the source, which
for our purposes is also called the target. Exitance has units
of W/m2. For thermal radiators, exitance is given
by the Stefan-Boltzmann law, namely
M = esT4.
Incidance, E. The flux per unit area at the detector.
Incidance, like exitance, has units of W/m2.
Fundamental to the process of detection is the relationship
between the incidence (E) and the exitance (M). Ultimately, to
quantify the detection ability of a receiver, we must derive a
transfer equation, which relates the two quantities E and M.
As this point the relationship is unknown, but to illustrate
what we want, we may write an expression:
E = (?) M,
where (?) represents some unknown (at this time) transfer function,
the parameters of which are yet to be determined. As you may
guess, it certainly will depend on the area of the target and
detector as well as the range between them. To proceed further,
we now must make some simplifying assumptions.
Spreading
The thermal radiation that is leaving the surface of the
target is distributed in all directions. Depending on the shape
of the object, some directions may have more or less radiation
than others. In the general case, it is not possible to know
the complete distribution of radiation as a function of direction
without detailed knowledge of the surface of the target. However,
there are two idealized shapes that can be used to make predictions.
Point Source
If there is no preferred direction, the thermal radiation
will be evenly distributed in all directions. In other words,
there is complete spherical symmetry. For example, if the target
were a ball, it would radiate equally in all directions. In this
case, it is as if the radiation where coming from a point at the
center of the object.
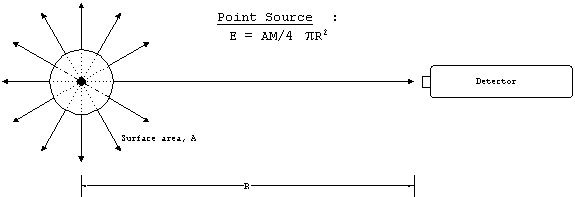
The transfer relation has a factor of 1/4pR2
which accounts for the spreading of energy in all directions,
and a factor which is the surface area of the source, A. The
point source model applies well to long range detection problems,
where the object appears small in the field-of-view of the detector.
At shorter ranges, where the source appears as an extended object,
we must use a different model.
Lambertian Source
When the source is large and/or close to the detector
it will appear as an extended object, and different areas on the
surface will come into the detector at different angles of incidence.
To the detector, the object will appear as a two-dimensional
object (i.e. flat), with an area equal to the projection of the
surface area in the direction of the detector. In order to not
have to worry about the exact three-dimensional shape of these
objects, the source is therefore modeled as a flat plate, perpendicular
to the detector, with the area of the plate equal to the projected
area of the object in that direction. Furthermore, we assume
that the radiation is emitted equally in all directions which
leads to a slight modification of one of the numerical factors
in the transfer relation. An object which can be modeled in this
manner is known as a Lambertian source. The defining characteristic
of a Lambertian source, is that all areas on the surface radiate
equally brightly regardless of where on the surface they are.
For example, the sun appears as a bright disk, with equal brightness
all areas on its surface.
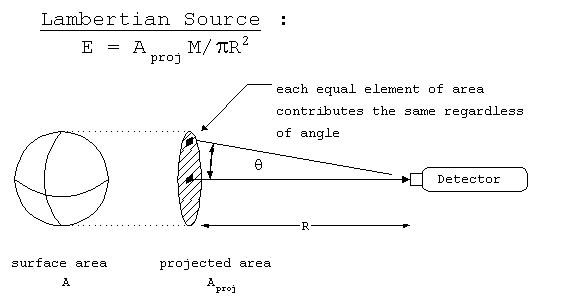
Figure 2. Lambertian source
geometry.
The transfer relation for a Lambertian source uses the projected
area of the source, Aproj, and is missing the factor
of 4 as compared to a point source. We may compare the two formulations
for a perfectly spherical source, which should yield the same
results. For a sphere of radius a, the surface area A = 4pa2.
The projected area Aproj = pa2.
Hence, when these terms are used in the respective equations
the factor of four is recovered and they are identical. Note
that this will not be true for other shapes, like a cube, where
the projected area is 1/6 of the total surface area, for example.
So far we have established two transfer equations, one
for a point source and the other for an extended source. They
are summarized below:
E = (A/4pR2)M, for a point
source
and
E = (Aproj /pR2)
M, for an extended (Lambertian) source.
Absorption/scattering
In the previous discussion, the transfer relation was
derived on the basis of purely geometrical concepts. However,
it is not true that all of the radiated energy can be captured
by detectors. The intervening medium between the source and the
detector, namely the atmosphere, will scatter and possibly absorb
some of the energy passing through it. The overall loss in the
flux is called attenuation, and is determined a variety
of factors. Primarily the attenuation is a function of the wavelength
and range. Additionally, it will depend on the nature of the
atmosphere, such as the humidity, visibility, weather and so forth,
but these factors are too variable to treat to other than empirically.
Dependence of Attenuation on Wavelength
The atmosphere is made up of a mixture of gases, predominately
nitrogen and oxygen. Here is the typical composition of dry air:
| Constituent | Volume % |
| Nitrogen, N2 | 78 |
| Oxygen, O2 | 20.9 |
| Argon, Ar | .9 |
| Carbon dioxide, CO2 |
.04 (variable) |
| Water vapor, H2O |
0-2 (variable) |
Table 1. Atmospheric constituents.
As in the case of selective radiators, these molecules can only
absorb energy at certain wavelengths. Although nitrogen and oxygen
are by far the most abundant, they do not absorb strongly in the
infrared spectrum. Only water vapor and carbon dioxide play a
significant role. They appear in varying amounts and therefore
one can expect a variation in the amount of attenuation. Of particular
note is the strong absorption by water vapor for wavelengths in
the 6-8 mm band. The corresponding
characteristic temperatures (i.e. the temperature which gives
has these values for the peak wavelengths) are 90-210 0C.
This makes detection of sources within this temperature band
difficult.
Dependence of Attenuation on Range (Bouguer's Law)
The amount of attenuation by the intervening atmosphere
will depend on the amount of flux. In general, the higher the
flux, the greater the losses. This is similar to radioactive
decay, where the decay rate is proportional to the amount of material
present. In both cases, the differential equation may be solved
and results in an exponential loss law. For electro-optics, this
is known as Bouguer's law which states that the fraction of flux
that is remains after attenuation, t,
is a function of range, R:
t = e-bR
where b is the extinction coefficient,
and has units of m-1. The factor t
is known as the transmission coefficient, and is dimensionless.
As short range, t will be close to
1.0 but will decrease and the range increases. At long range,
t will be nearly zero.
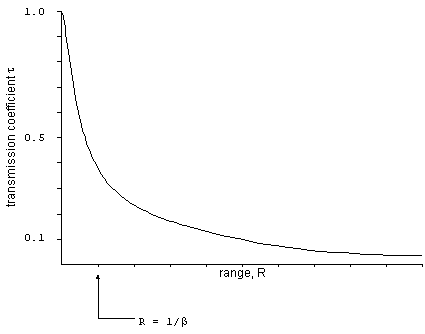
The extinction coefficient determines the range at which the transmitted
flux is significantly reduced. When the range is 1/b,
the transmission coefficient will be 0.37. The extinction coefficient
will generally be different for each detector, since the band
of wavelengths each detector looks at are usually different.
Furthermore, it will depend on the exact atmospheric conditions,
including weather, season, time of day, and altitude. Here some
typical values:
| Band (mm) | Extinction coefficient, b |
| 3-5 | 6.7 x 10-5 m-1 |
| 8-12 | 2.0 x 10-4 m-1 |
Table 2. Extinction coefficients.
The transmission coefficient, t, can
be used directly in the transfer relation. For example, for a
point source, the incidance is (note that t
is a function of range):
E = (tA/4pR2)M.
The Collected Flux
Aperture
The incidance, E, represents the power per unit area that arrives
at the detector. As a rough estimate, one could multiply the
incidance by the size of the opening to the detector to determine
the amount of flux that gets collected by the detector. However,
this process is not 100% efficient. Some of the flux may be reflected,
scattered or absorbed by the materials. Therefore, in complete
analogy with our discussion of radar, we can define the effective
area for collecting the incidance, which is also called the detection
aperture, given the symbol Ae. The aperture is
defined by:
Ae = rA
where:
r = the efficiency of the collection
for the detecting system, and
A = the physical size of the opening into the detector.
The physical opening into the detector can be limited
by an aperture stop (A.S.), which is physical barrier at
the entrance of the detector. The aperture stop will limit the
amount of flux that can enter the detector, but in turn can improve
the depth of focus (which will be discussed in the next chapter).
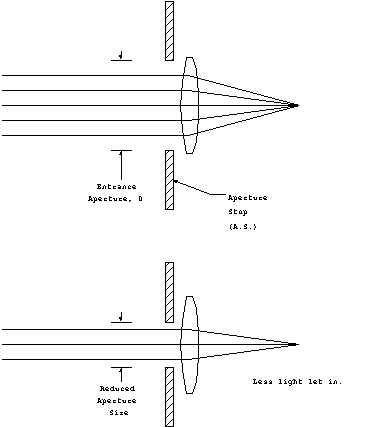
affects the collected flux.
For a given aperture, Ae, the amount of flux that will
be collected by the receiver is the product of the incidance and
the aperture:
Fcollected = Ae
E
Bandwidth Factor, F
Thermal radiators emit their energy over a wide band of
wavelengths. In general it is not possible to design a detector
which will be equally sensitive over all the wavelengths in this
range. Therefore, there will be some upper and lower bounds on
the wavelengths that can be detected. Designate these bounds as
lupper and llower.
For our purposes, we assume that the detector can pick up any
energy that is within this range, and nothing that is outside
of it. Since the spectrum of the radiation from a thermal emitter
will not all be within the detection band, we define the bandwidth
factor, F, to be the fraction of the radiation that is within
the detector band.
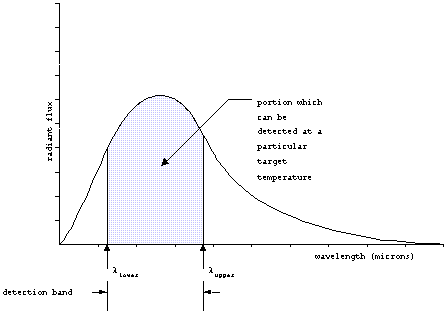
The detector bandwidth factor, F, could be obtained by
integrating the flux vs. wavelength curve for the source between
the limits of wavelengths for the detector. This curve varies
with target temperature, so it is useful to remove this dependence.
The universal black-body curve represents the fraction of the
total flux which is outside of the band from zero to the new variable
lT, in units of mm-K.
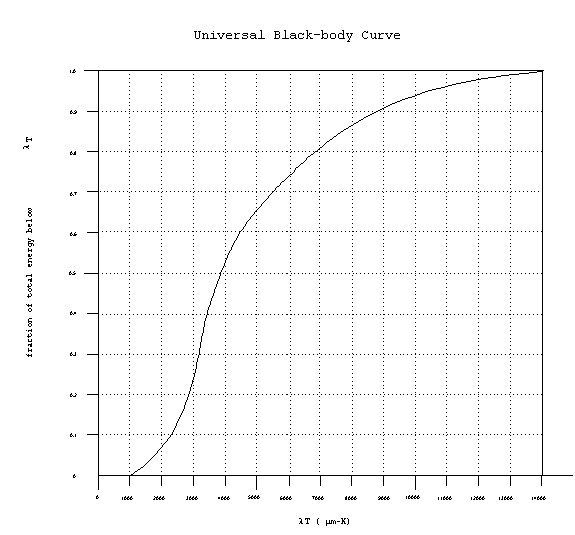
Figure 6. Universal black-body
curve.
Since the variable lT now carries the
temperature dependence this curve can be used for all sources.
The bandwidth factor F can be found by using the curve twice:
once for the lower limit and once for the upper limit, the difference
being the desired factor F. This process is best illustrated
by the following example.
Example: find the bandwidth factor for a detector operating between
2 and 6 microns, for a target at 500 K.
First, find the fraction of flux outside of the band from 0 to
1000 mm-K (corresponding to the smallest
wavelength detectable, 2mm times the
temperature, 500 K),
fraction below 0-1000 mm-K: 0.0 (i.e.
nothing is detected)
Secondly, find the fraction of the flux below the band from 0
to 3000 mm-K (corresponding to the
largest wavelength detectable).
fraction below of 0-3000 mm-K: 0.25
Therefore, the fraction of the total flux within the band of 1000
to 3000 mm-K is 0.25 - 0.00 = 0.25,
or 25%
F = 0.25
Given the bandwidth factor, F, the flux collected and
dtectable by the receiver is now:
Freceiver = FAeE.
Maximum Range Equation
Having discussed all the preliminaries, we can now put
it all together and predict the maximum range at which infrared
detection can take place. Similarly to radar, let Smin
represent the minimum flux that the receiver can detect. Then
the detection criterion can be written as
Freceiver > Smin,
for successful detection.
Since the amount of flux at the receiver decreases with range,
we can define the detection criterion at maximum range, where
Freceiver = Smin,
using the previously derived expressions:
Freceiver = AT
M F Ae/(4p R2max)
= Smin
Which can be solved for Rmax. Finally we substitute
in the Stefan-Boltzmann law for exitance M and obtain:
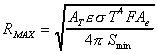
range in vacuum.
Note that the factor for atmospheric attenuation, t,
has been omitted from this equation. Recall that the atmospheric
attenuation is a function of range. This would make it impossible
to write an equation for range in a closed-form. Therefore, the
maximum range that is predicted by this formula, does not include
atmospheric attenuation. This factor can be included as a correction,
using numerical or graphical means to solve for the true range.
If the predominant source of noise is the background environment,
the detector is said to background-limited. In this case
Smin will depend on the temperature of the target in
relation to the background. Not only will a higher temperature
increase the contrast between the target and the background, but
will also serve to separate their spectra as the peak wavelength
shortens.
If the predominant source of noise is the detector itself,
the detector is said to be noise-limited. In this, the
minimum flux can be written as
Smin = (S/N) NEP
where:
S/N = the signal-to-noise ratio required for detection, and
NEP = the noise-equivalent power.
Example: find the maximum detection range for a point-source
target, with surface area 2 m2, emissivity of 0.95
and temperature of 500 K, given the following detector characteristics:
Aperture = 0.1 m2
Detection band = 2-6 mm
Smin = 6 x 10-7 W
Step 1: Compute F, using the universal black-body curve with
arguments of 1000 and 6000 mm-K F
= 0.75
Step 2: Calculate range
R = 8190 m