
Table of
Contents
 Table of Contents |
As a first step in developing an understanding of the medical implications of nuclear warfare, it is essential to understand how a nuclear weapon differs from a conventional high explosive weapon. Accordingly, a comparison will be made in this chapter between the mechanisms of energy production in conventional and nuclear detonations. In addition, certain principles of atomic structure and physics are presented to aid in the understanding of these differences.
An explosion can be described as the sudden release of large amounts of energy within a limited space as the system involved is converted to a more stable one. The basic laws of thermodynamics pertaining to the conservation of energy require that energy must be released when a system is converted to another of greater stability, i.e., one containing less energy.
203. Conventional Chemical Explosion.
a. The molecules of conventional chemical explosives are considered to be in a high- energy or unstable state. When such a system is made to react, products of greater stability are formed and energy is released. With a conventional explosive, such as trinitrotuluene (TNT), the energy is derived from a sudden, violent chemical reaction, altering various bonds between the molecules of the explosive's chemical compounds, i.e.,
2 Molecules TNT + Heat = Reaction Products + Energy
The amount of energy released in such a reaction is directly proportional to the difference between the total binding energy contained within the initial, unstable system and that contained within the final, more stable system. This net energy release is called the heat of explosion.
b. As in all chemical reactions, mass and energy are conserved separately; i.e., by the best methods of measurement available, the total mass and the total energy, including the heat of explosion, are found to be exactly the same, respectively, before and after the explosion.
Energy released in a nuclear explosion is not produced by chemical reactions. Rather, it results from so-called nuclear reaction, fission and fusion, in which fundamental changes occur in the composition of the nuclei of the reacting material rather than in the electron shells as is the case in chemical reactions. In these nuclear reactions mass is actually converted to energy, and the amount of energy produced is many orders of magnitude greater than that available from chemical reactions. To fully appreciate the nature of these reactions, certain basic concepts related to atomic structure and nuclear reactions must first be understood.
a. Elements. All substances are composed of one or more of over 100 different kinds of basic materials known as elements. There are 92 naturally occurring and at least 11 artificially produced elements, ranging from the simplest and lightest naturally occurring element hydrogen to the heaviest artificial element lawrencium.
b. Atomic Structure. The simplest structural unit of any element that can exist, while still retaining the chemical and physical characteristics of the element, is called an atom. An atom is composed of a central nucleus containing most of its mass and electrons orbiting in shells around the nucleus (Figure 2-I). The nucleus consists of a number of fundamental particles, the most important of which are the protons and neutrons.
(1) The proton is a particle having a positive charge, equal in magnitude and opposite in sign to that of the electron. The proton's mass is approximately 1845 times greater than that of the electron.
(2) The neutron is an uncharged particle having a mass slightly greater than that of the proton, approximately equal to the sum of the masses of a proton and an electron.
(3) Electrons are negatively charged particles. They orbit the nucleus at discrete energy levels referred to as electron shells.
c. Electrical Charge. Atoms are electrically neutral when the number of negatively charged electrons orbiting the nucleus equals the number of positively charged protons within the nucleus. When the number of electrons is greater than or less than the number of protons in the nucleus, atoms are not electrically neutral and carry a net negative or positive charge. They are then termed ions and are chemically reactive, tending to combine with other ions of opposite net charge. When atoms are combined in molecules, they may share electrons to achieve stability of electron shell structure (Figure 2-II).
a. Atoms of different elements have different numbers of protons in their nuclei. The term atomic number describes the number of protons in a nucleus. Although all the nuclei of a given element will have the same atomic number, they may have different atomic masses because they may contain different numbers of neutrons. Generally, this does not affect the chemical properties of the different atoms since the numbers of protons are not changed but does have profound effects upon nuclear stability of the different atoms. The total number of protons and neutrons in an atomic nucleus is referred to as the atomic mass number. Atomic species which have identical atomic numbers but different atomic mass numbers are called isotopes (Figure 2-III).
b. The stable isotopes of elements have very definite ratios of neutrons to protons in their nuclei. As atomic mass numbers increase, the ratio of neutrons to protons increases according to a definite pattern (Figure 2-IV). If isotopes vary from this pattern, they are relatively unstable.
a. Common units of mass, such as grams, are much too large to conveniently describe the mass of an atomic nucleus or any of its constituent parts. To solve this problem a new unit was defined: the atomic mass unit (amu). The atomic mass unit is a relative unit defined arbitrarily by assigning a mass of 12 amu to the neutral atom carbon-12, the common isotope of carbon. One atomic mass unit equals 1.66 X 10-24 grams. Employing this value, the masses of the fundamental particles of an atom have been determined to be:
(1) Proton mass: 1.00727 amu.
(2) Neutron mass: 1.00867 amu.
(3) Electron mass: 0.00055 amu.
b. Logically, it should be possible, knowing the number of particles comprising a particular atom, to calculate the mass of that atom. However, experiments have shown that the total mass of an atom is less than the sum of the masses of the atom's electrons, protons, and neutrons. For example, the measured mass of the isotope fluorine-19 atom is 18.99840 amu, while the sum of the masses calculated for the individual particles of that atom is 19.15708 amu. The difference of 0.15868 amu between the measured and calculated mass of the fluorine-19 atom is defined as the mass defect (Figure 2-V).
c. Careful experimentation and study have shown that while the mass defect is real, the law of conservation of mass has not been violated. When basic particles combine to form an atom, a certain amount of mass is lost through conversion into energy in accordance with Einstein's equation E = mc2, where E is the energy, m is the mass, and c is the velocity of light in a vacuum. The converted energy is considered to be binding energy, i.e., energy necessary to hold the nucleus together.
a. A standard notational form is used to identify the individual isotopes of a given element. The standard notation takes the following form:
|
A |
|
|
|
X |
|
Z |
where X = chemical symbol of the element, Z = atomic number, and A = atomic mass number.
b. An example of the standard notation would be:
|
235 |
|
|
|
U |
|
92 |
c. Reference to a chart of the nuclides would reveal that the element with an atomic number of 92 is uranium, the chemical symbol for which is U. The atomic mass number 235 identifies a uranium isotope having 92 protons and 143 neutrons (235 - 92 = 143) in its nucleus. Thus the isotope identified by the example notation is the naturally occurring, readily fissionable isotope of uranium used in nuclear weapons. The atomic number is frequently left off, and such an isotope may then be represented only by its mass number and chemical symbol, i.e., 235U.
a. Fission is a nuclear process in which a heavier unstable nucleus divides or splits into two or more lighter nuclei, with the release of substantial amounts of energy. The materials used to produce nuclear explosions by fission are those isotopes of uranium or plutonium which undergo fission most readily. These are 235U and 239Pu. When as illustrated in Figure 2-VI, a free neutron of the proper energy is captured by the nucleus of a fissionable atom, the resulting unstable nucleus will "split" producing two or more fission products (atoms of different elements formed from the protons, neutrons, and electrons originally comprising the nucleus before its fission), two or three free neutrons and a tremendous amount of energy.
b. In terms of continued energy production, the most significant point about the fission process is the emission of free neutrons, which can in turn produce other fission events, which in turn produce still another generation of free neutrons. Each generation of fission produced neutrons can produce a large number of fissions; and so, within a few generations, the total number of fissions produced can be tremendous.
c. While in principle a single neutron could initiate a chain reaction of nuclear fissions which could ultimately result in the splitting of each fissionable atom in a given mass, not all of the neutrons produce more fissions. Some of the neutrons may escape from the fissionable mass. Others may be removed by nonfission reactions. To initiate a chain reaction, sustain that reaction for a period sufficiently long to permit a buildup of explosive energy, and confine the released energy for as long as possible to maximize the weapon's explosive effect requires that a variety of special conditions be met.
The first prerequisite to be met in producing a fission-type nuclear explosion is that there must be enough material present and in the right configuration so that successive generations of neutrons can cause equal or increased numbers of fissions. The amount capable of sustaining a continuous or chain reaction is termed a critical mass.
a. Although fission events release more than 2 million times more energy per event than do chemical reactions, there still must be a tremendous number of fissions to result in the release of a significant amount of energy. To meet this requirement, a mass of fissionable material having specific characteristics must be assembled. Depending on size, and other factors to be discussed, a given mass of fissionable material may support one of three types of chain reactions:
(1) Subcritical Chain Reaction. A reaction in which the number of neutrons decreases in succeeding generations, thus not continuing.
(2) Critical Chain Reaction. A reaction in which the number of neutrons remains constant in succeeding generations.
(3) Supercritical Chain Reaction. A reaction in which the number of neutrons increases in succeeding generations.
b. To produce a nuclear explosion, a weapon must contain an amount of uranium or plutonium that exceeds the mass necessary to support a critical chain reaction, i.e., a supercritical mass of fissionable material is required. Several methods can be used to make a mass of fissionable material supercritical.
(1) The active material can be purified to eliminate unwanted chemical impurities that might otherwise absorb neutrons.
(2) Fissionable material can be enriched, i.e., the amount of 235U as compared to 238U can be increased.
(3) The material can be machined into the most efficient shape. A spherical shape can be employed to provide the greatest volume with the least surface area, thereby reducing the probability of neutron loss.
(4) Moderators can be used to slow down fission neutrons, increasing the probability of their producing fissions.
(5) Finally, neutrons that have escaped the active material can be reflected back by using suitable materials as reflectors. Reflectors, used as tampers, can also physically delay the expansion of the exploding material allowing more fission to occur thereby resulting in an increase in explosive energy.
c. Because of the stray neutrons produced in the environment by spontaneous fission, those present in the atmosphere from cosmic ray interactions as well as others generated in various ways, a critical or supercritical mass would be likely to melt or possibly explode. It is necessary, therefore, that, before detonation, a nuclear weapon contain no piece of fissionable material as large as a critical mass. At the time of the detonation, some method must be employed to make the mass supercritical by changing its configuration. Two general methods have been developed for quickly converting a subcritical mass into a supercritical one.
(1) In the first, two pieces of fissionable material, each less than a critical mass, are brought together very rapidly to forma single supercritical one. This gun-type assembly may be achieved in a tubular device in which a high explosive is used to blow one subcritical piece of fissionable material from one end of the tube into another subcritical piece held at the opposite end of the tube (Figure 2-VII).
(2) In the second or implosion-type assembly method (see Figure 2-VIII), a subcritical mass of 235U or 239PU is compressed to produce a mass capable of supporting a supercritical chain reaction. This compression is achieved by the detonation of specially designed high explosives surrounding a subcritical sphere of fissionable material. When the high explosive is detonated, an inwardly directed implosion wave is produced. This wave compresses the sphere of fissionable material. The decrease in surface to volume ratio of this compressed mass plus its increased density is then such as to make the mass supercritical. An enhanced radiation (ER) weapon, by special design techniques, has an output in which neutrons and x-rays are made to constitute a substantial portion of the total energy released. For example, a standard fission weapon's total energy output would be partitioned as follows: 50% as blast; 35% as thermal energy; and 15% as nuclear radiation. An ER weapon's total energy would be partitioned as follows: 30% as blast; 20% as thermal; and 50% as nuclear radiation. Thus, a 3-kiloton ER weapon will produce the nuclear radiation of a 10-kiloton fission weapon and the blast and thermal radiation of a 1-kiloton fission device (Figure 2-IX). However, the energy distribution percentages of nuclear weapons are a function of yield.
In general, fusion may be regarded as the opposite of fission. It is the combining of two light nuclei to form a heavier nucleus. For the fusion process to take place, two nuclei must be forced together by enough energy so that the strong, attractive, short-range, nuclear forces overcome the electrostatic forces of repulsion. The two conditions necessary for the fusion of appreciable numbers of nuclei are high temperatures to accelerate the nuclei and high pressure density to increase the probability of interaction. The only practical way to obtain the temperatures and pressures required is by means of a fission explosion. Consequently, weapons with fusion components must contain a basic fission component. The energy released in the explosion of a fission-fusion weapon originates in approximately equal amounts from the fission and fusion processes.
Paragraph 208c. described the isotope 235U as being "... the naturally occurring, readily fissionable isotope of uranium..." An expanded, but more complete, description would also have identified the isotope 235U as being radioactive. Similarly, in a fission reaction most, if not all, of the fission products produced are radioactive.
The nuclei of certain naturally occurring isotopes, and of others produced artificially, contain excess energy, i.e., they are unstable. To attain stability, nuclei with excess energy emit that energy in the form of nuclear, ionizing radiation and, in that process, frequently change into different elements. (See paragraph 215e.) (Ionizing radiation is defined as radiation capable of removing an electron from a target atom or molecule, forming an ion pair.) Isotopes, the nuclei of which emit ionizing radiations to achieve stability, are termed radioactive. Radioactive isotopes are referred to as radioisotopes or radionuclides.
a. Radioactive Decay. The process wherein radionuclides emit ionizing radiation is also termed radioactive decay. Each radioisotope has its own characteristic decay scheme. A decay scheme identifies the type or types ionizing radiation emitted; the range of energies of the radiation emitted; and the decaying radioisotope's half-life.
b. Half-Life. Half-life is defined as the time required for half of the atoms of a given sample of radioisotope to decay. Half-life values range from fractions of a millionth of a second to billions of years. Theoretically, no matter how many half-lives have passed, some small number of nuclei would remain. However, since any given sample of radioactive material contains a finite number of atoms, it is possible for all of the atoms eventually to decay.
c. Data Plotting. Radioactive decay may be plotted in a linear form as shown in Figure 2-X or in a semilogarithmic form as in Figure 2-XI. The latter has the advantage of being a straight lineplot. The straight line form is used extensively in radiation physics, particularly when dealing with isotopes with short half-lives, since it allows direct determination by simple inspection of the activity at any given time with a precision adequate for most purposes.
a. The international system of units is based on the meter, kilogram, and the second as units of length, mass, and time, and is known as Systems International (SI). The amount of radioactivity in a given sample of radioisotope is expressed by the new Systems International (SI) unit of the Becquerel (Bq). The old unit was the Curie (Ci). One Becquerel of a radioisotope is the exact quantity that produces one disintegration per second. The Curie is 3.7 x 1010Bq disintegrations per second. Thus 1 Bq = 2.7 x 10-11Ci and 1 Ci = 3.7 x 1010Bq. As the Becquerel is inconveniently small for many uses as was the Curie inconveniently large, prefixes such as micro (µ) (10-6), milli (m) (10-3), kilo (k) (103), mega (M) (106), and giga (G) (109) are routinely used. Following nuclear detonations, the amounts of radioactive material produced are very large and the terms pets-becquerel (PBq) (1015Bq) and exabecquerel (EBq) (10l8Bq) may be used. The term megacurie (MCi) (106Ci) used to be used.
b. The amount of radioactive material available at any time can be calculated by using a specific mathematical formula:
from which the following can be derived
since |
c. The terms in these formulae are as follows:
(1) At = activity remaining after a time interval, t.
(2) Ao = activity of sample at some original time.
(3) e = base of natural logarithms (2.718...).
(4)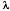 = decay constant of the particular isotope, derived from the half-life.
= decay constant of the particular isotope, derived from the half-life.
(5) t = elapsed time.
(6) T1/2 = half-life of the particular isotope.
d. This formula can be used to calculate the activity (A) of an isotope after a specific time interval (t) if the half-life (T1/2) and the original activity (Ao) are known.
(1) Example: If 3.7 x 1010Bq (= 1.0 Ci) of 6oCo (cobalt) is the original amount of radioactive material at time to, what will be the activity of the 60Co remaining 1 month later?
A1 month = activity remaining after 1 month (t)
A0= 3.7 x = 10 10Bq (original activity)
T1/2 = 5.27 years (half-life of 60Co is 5.27 years)
t = 1 month (time elapsed since the original time).
(2) Substituting in the formula gives the following:
(4) In other words, the activity of 60Co after 1 month is 0.99 of its original activity, a reduction of only 1%. This could not be determined with precision from a graphic plot of activity versus time.
Radioisotopes of heavy elements such as radium or uranium characteristically decay by emission if ionizing radiation in the form of alpha particles. Some heavy elements also decay by spontaneous fission which results in neutron releases. For the lighter elements, emission of beta particles is common. In addition, emissions of gamma or x-ray photons almost invariably accompany both alpha and beta particle radiation. This is important since gamma or x radiation constitutes the principal casualty producing form of ionizing electromagnetic radiation associated with nuclear explosions. X-ray and gamma photons are essentially identical, differing only in their points of origin. Gamma photons originate in the nuclei of decaying atoms while x- rays originate in the electron shells surrounding nuclei. Refer to paragraphs 503-506 for detail of penetration capabilities of the types of radiation.
a. Even though they possess no net electrical charge, gamma and x-ray photons interact with atoms to produce ionization. Gamma photons have discrete energies over a very wide range, but are considerably less ionizing than alpha or beta particles but much more penetrating.
b. An alpha particle is a helium nucleus consisting of two protons and two neutrons all strongly bound together by nuclear forces. Alpha particles have a mass about 7000 times that of electrons and are ejected from the nuclei of radioactive atoms with one, or at the most several, characteristic and discrete energies. Although highly ionizing, alpha particles are only slightly penetrating.
c. Beta particle decay involves the conversion of a neutron into a proton and electron within the nucleus. While the proton is retained in the nucleus, the beta particle (electron) is ejected with a velocity dependent upon its kinetic energy. Opposed to alpha particles, beta particles show a continuous energy spectrum. Because of its smaller mass and relatively higher emission energies, a beta particle is less ionizing than an alpha particle but more penetrating.
d. In a fission process, neutrons are also released and consequently, make up a significant portion of the total radiation output.
e. From the discussion in paragraphs 215b and 215c, it can be seen that, depending upon the type of particulate radiation emitted in decay, decaying nuclei can, in addition to changing their energy states, be transformed into new elements. Examples of the transformation resulting from alpha and beta particle decay are shown in Table 2-I.
a. Ionizing radiation interacts with matter in one of two ways. It is either scattered or absorbed. Both result in deposition of energy in the target system. The mechanisms of absorption are of particular interest because:
(1) Absorption in body tissue may result in physiological injury.
(2) Absorption is a phenomenon upon which the detection of ionizing radiation is based.
(3) The degree of absorption or type of interaction is a primary factor in determining shielding requirements.
b. Transfer of energy from an incident photon or particle to the atoms of an absorbing target material may occur by several mechanisms.
(1) Excitation. This process involves the addition of energy to an atomic or molecular system, thereby transferring it from its ground or stable state to an excited or unstable state. Depending upon the type of interaction, either the atomic nucleus or one of its orbital electrons may absorb the excitation energy.
(a) Electron excitation occurs when relatively small amounts of energy are transferred. Here the electrons may only be moved to a higher energy level in the atom (Figure 2-XII).
(b) An excited electron will not retain its energy but will tend to return to its original energy level either by emitting the excess energy in the form of a photon of electromagnetic radiation (x-ray) or by transferring its energy to the electrons of other atoms or molecules.
(2) Ionization. As indicated previously, ionization is any process which results in the removal of an electron (negative charge) from an atom or molecule thereby leaving the atom or molecule with a net positive charge. Ionization occurs if alpha or beta particles, or gamma photons transfer sufficient energy to dislodge one of the electrons from the outer orbital shells of the target atom. Each ionization event produces an ion pair consisting of a free electron and the positively charged remainder of the atom (Figure 2-XIII).
In terms of ionization, gamma radiation interacts with matter via three main processes: photoelectric effect, Compton scattering, and pair production.
a. Photoelectric Effect. This describes the case in which a gamma photon interacts with and transfers all of its energy to an orbiting electron, ejecting that electron from the atom (Figure 2-XIV). The kinetic energy of the resulting photoelectron is equal to the energy of the incident gamma photon minus the binding energy of the electron. The photoelectric effect is thought to be the dominant energy transfer mechanism for x-ray and gamma ray photons with energies below 50 keV (thousand electron volts), but it is much less important at higher energies.
b. Compton Scattering. This is an interaction in which an incident gamma photon loses enough energy to an orbital electron to cause its ejection, with the remainder of the original photon's energy being emitted as a new, lower energy gamma photon with an emission direction different from that of the incident gamma photon (Figure 2-XV). The probability of Compton scatter decreases with increasing photon energy. Compton scattering is thought to be the principal absorption mechanism for gamma rays in the intermediate energy range 100 keV to 10 MeV (million electron volts), an energy spectrum which includes most gamma radiation present in a nuclear explosion. Compton scattering is relatively independent of the atomic number of the absorbing material.
c. Pair Production. By interaction in the vicinity of the coulomb force of the nucleus, the energy of the incident photon is spontaneously converted into the mass of an electron-positron pair. A positron is a positively charged electron. Energy in excess of the equivalent rest mass of the two particles (1.02 MeV) appears as the kinetic energy of the pair and the recoil nucleus. The electron of the pair, frequently referred to as the secondary electron, is densely ionizing. The positron has a very short lifetime. It combines with 10-8 seconds with a free electron. The entire mass of these two particles is then converted to two gamma photons of 0.51 MeV energy each (Figure 2-XVI).
a. Due to the high probability of interaction between an alpha particle and orbital electrons in an absorbing medium, a large number of ion pairs are formed per unit path length. Since a finite fraction of the total kinetic energy of an alpha particle is absorbed with the formation of each ion pair, the alpha particle will lose its energy over a relatively short distance. For these reasons, the range of alpha particles is much less than the range of beta particles or gamma photons.
b. Beta particles and orbital electrons have negative charges, resulting in electrostatic repulsion when in the vicinity of one another. But, a beta particle has a charge opposite to that of the atomic nucleus, resulting in electrostatic attraction. Normally a beta particle loses its energy in a large number of ionization and excitation events in a manner analogous to the alpha particle. However, the range of the beta particle is considerably greater than that of an alpha particle. The beta particle travels longer distances between interactions and follows a "drunken man's path" through matter.
a. The penetrating ability of radiation depends on the rate at which the radiation deposits energy along its path. The term specific ionization, which is defined as the average number of ion pairs generated per unit length of path, is used to describe the ionizing capability of ionizing radiations.
b. Generally speaking, the ion density along the path of a low-energy particle is greater than that along the path of a high-energy particle of the same mass and charge. This is because the low-energy particle is moving slower and has more time to interact. Its total pathway is shorter, however, and the total number of interactions may well be less. Likewise, the ion density towards the end of the path of a particle is greater than at the beginning, because its velocity is less and the probability of interaction is increased accordingly. Alpha particles are capable of producing the highest specific ionization followed in order by beta particles and the secondary electrons produced by gamma-photon interactions (Table 2-II).
c. The more common basis for comparing the various types of radiations is known as Linear Energy Transfer (LET), and represents the average energy released (or lost) per unit track length in ionization and excitation interactions. LET is usually expressed in units of KeV (thousands of electron volts) per micron of path length. To a considerable extent, the Relative Biological Effectiveness (RBE) of various radiations depends on the rate of energy loss (LET) along the paths of the individual ionizing particles or photons. Radiations with low LET such as x- or gamma rays produce diffuse ionizations throughout the medium. In contrast, the LET associated with neutrons or alpha particles is so high that the passage of a single track will, in all probability, put enough ionizations into a traversed cell to produce death.
The maximum ranges of ionizing radiation in matter depend not only on the characteristics of the specific particles or photons but also on the stopping power of the absorbing material. The stopping power of a material is a function of electron density or the number of electrons per unit volume of the substance and represents the total energy lost in collision and radiative interaction. The electron density increases as the density electrons per gram (1023). Materials differ in their stopping power on the basis of the ratio of their atomic number to their atomic mass (Z/A) times the density of the material. The range of a charged particle in an absorbing material is inversely proportional to this ratio. For example, if the range of a given energy beta particle is 1 cm in water, its range in air would be much greater (about 10 m), and in iron much smaller (about 1 mm).
a. The concept of stopping power is not generally used in connection with material interactions of either gamma photons or uncharged neutrons. Since high-energy radiation is in general more penetrating than low-energy radiation, the specification of half-value layer (HVL) is often a convenient method of characterizing the penetrating quality of an energy spectrum. Half-value layer is defined as that absorber thickness which reduces a given radiation intensity to one-half of the incident value (Figure 2-XVII). Refer to Table 7-II for half-value layer thickness of common materials.
b. The relatively high penetrating power of x and gamma radiation compared with charged particles is related to the fact that the absorption interactions are fairly rare occurrences. The attenuation of gamma radiation as it passes through matter can expressed by the following formula:
where:
(1) I = gamma radiation intensity after passing through a target material thickness d (see below).
(2) I0 = intensity of the incident gamma radiation at the surface of the target.
(3)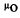 = material-dependent attenuation coefficient (cm-1).
= material-dependent attenuation coefficient (cm-1).
(4) d = thickness of the target material (cm).
Although most ionizing radiation injuries associated with nuclear warfare will be attributable to gamma radiation previously described, a sufficient number of high-energy fission neutrons escape from the detonation to represent a significant hazard at considerable ranges.
a. The neutron is a particle and thus is fundamentally different from electromagnetic radiation. It also differs from other particulate radiations (alpha and beta) in that neutrons do not carry any electrical charge. As a result, neutrons do not interact with the orbital electrons of atoms. Instead, they interact directly with the nuclei of atoms, particularly those having low atomic mass numbers.
b. Depending on their point of origin, neutrons may have energies ranging from a fraction of an electron volt (Ev) for so-called thermal neutrons to several megaelectron volts (MeV) for fast (fission) neutrons, to fusion neutrons which have energies of up to 14 MeV (e.g., deuterium-tritium reaction). Most neutrons produced in a nuclear fission detonation will have energies less than 1 MeV. A small fraction will have energies above 3 MeV. In enhanced radiation weapons, there will be a preponderance of 14 MeV neutrons.
c. Neutrons transfer their energy to target atoms and molecules by elastic and inelastic collisions with nuclei.
In elastic collisions, part of the neutron's energy is transferred to the target atom in a manner analogous to a purely mechanical collision process (Figure 2-XVIII).
a. Because the energy of a neutron is degraded by interactions with atomic nuclei, the probability of a neutron interacting with a target material does not depend on electron density as it does for other types of radiation. For fast neutrons, the probability of collision is practically the same for all nuclei. Since, in accordance with the laws of mechanics, considerably more energy is transferred in a collision between two objects of similar mass, neutrons will transfer more energy to target nuclei of substances of low atomic mass rather than to heavy nuclei. The lightest element is common hydrogen, 1H, the nucleus of which contains a single proton. The mass of a proton is essentially the same as that of a neutron; and so, when a neutron collides with a hydrogen nucleus it can lose a considerable fraction of its energy in the interaction. Therefore, substances containing large quantities of hydrogen are good neutron moderators.
b. The energy transfer mechanism with hydrogen accounts for more than 90% of the fast-neutron energy transfer up to 7 MeV occurring in wet, muscle-like tissue. The hydrogen nucleus then becomes ionized since it is accelerated away from its orbiting electron. An ion pair made up of the proton (H+) and the hydroxyl ion (OH-) is produced. The accelerated proton can, in turn, cause further secondary ionizations or excitations, spreading the damage of the original interaction. For neutrons with energies above 7 MeV, nuclear reactions with other tissue components become relatively important, but, even at 18 MeV, elastic scattering of protons constitutes about 70% of the energy absorbed in tissue.
In inelastic collisions a neutron is captured by the target nucleus and a neutron of much lower energy is emitted leaving the target nucleus in an excited state. This energy is subsequently emitted in the form of electromagnetic radiation (Figure 2-XIX).
a. Thus, in inelastic collisions or capture the incident neutron energy is absorbed entirely. Much of it appears as subsequent electromagnetic radiation which is high penetrating and can interact with the target at some other location. (See discussion on photon interactions.)
b. Because the nucleus of an atom occupies so small a fraction of the total atomic volume, the probability of either elastic or inelastic scattering along a given neutron's path is very small. Even so, the energy transfer from an inelastic collision is significantly greater than that seen in the ionization or excitation interactions of gamma photons in tissue, and the penetrating ability of a fission-energy neutron is significantly less than that of gamma photons.
c. A wide variety of interactions of neutrons with elements present in tissues is possible. Incident neutrons of relatively low energy interact with and are captured by the nuclei of tissue elements, which become activated and emit a photon (gamma ray), which can penetrate over considerable distances prior to electron interactions. In interactions initiated by higher energy neutrons, the reaction products may have various energies depending on the energy level involved. Various biological materials have been used or suggested for measurements in connections with accidental exposure to neutrons. 32P activity in body hair has been employed in the evaluation of exposures to neutrons. Both blood and whole body measurements of 24Na activity are also important in the more accurate assessment of absorbed dose.
a. The total dose due to initial radiation from a nuclear weapon can be divided into two components, neutrons and gamma rays. The neutron-to-gamma ratio is the ratio of neutron dose to gamma dose present at a specified point. The neutron-to-gamma ratio for a given total dose level is dependent on weapon yield and design, air density, and height-of-burst (HOB). Some typical neutron-to-gamma ratio values for 2600 centiGray (cGy) total dose to an unprotected individual are shown in Table 2-III.
b. As a general rule, the neutron-to-gamma ratio decreases with the range from the weapon's ground zero. This is due to the neutrons interacting with the air, creating secondary gamma. As a result, the gamma component decreases at a slower rate than does the neutron component. Thus, the ratios would be lower than the above values for a given yield at the 50-150 cGy dose levels because of the increased distance. These dose levels are typical of safety criteria. The ratios for vehicles and shelters depend on the specific neutron and gamma protection factors associated with the vehicle or shelter. These factors are based on the material used in construction. There are no typical ratios for vehicles, since each component of the ratio is effected differently by the associated radiation protection factor. However, for a tank, the protection factors are about 2 and 10 for neutrons and gammas, respectively. In other words, the neutron component would be decreased by a factor of two. Therefore, at least for tanks, the gamma radiation is more effectively stopped. This will significantly effect the neutron-to-gamma ratio within the vehicle. In this case, the neutron-to-gamma ratio would increase.